Aller au contenu

Verify Robust Positive Invariance with Enclosing Method

This page presents a Python code to demonstrate the enclosing method in 2 simple examples. This numerical method verifies the robust positive invariance (RPI) of an ellipsoid with respect to dynamical systems. The systems may be subject to bounded perturbations. RPI ellipsoids can be used to study the systems’ stability.

Download the python code: https://github.com/MLouedec/Demo_enclosing_method

Dependencies: sympy, numpy, scipy, random, math, codac, matplotlib, time

1st example, a simple damped pendulum

The first example studies the stability of a simple damped pendulum. Run: pendulum_example.py

Three state ellipsoids are tested: Q1 (RPI), Q2 (not RPI), and Q3 (too small to be verified RPI). The noise amplitude can be tuned with « Wi_box ». If the green ellipsoid (the result of the enclosing method) is in the red ellipsoid (Q1, Q2, or Q3), then the red ellipsoid is robust positive invariant. The blue curve simulates state trajectories. The results are visible below:

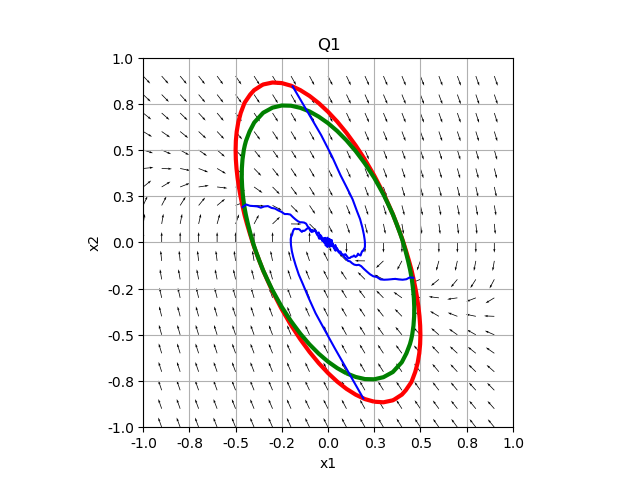
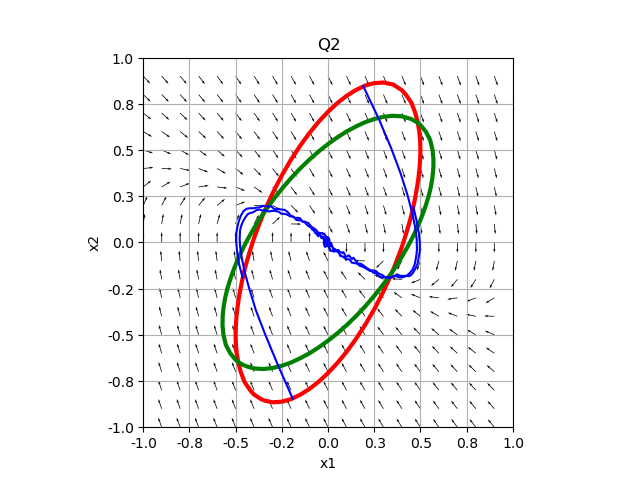
The results of the pendulum example with Q1 Q2 and Q3. The red ellipsoid is the candidate, the green ellipsoid is the Euler prediction of the candidate. The blue curves are simulated trajectories.

2nd example, platooning

The second example studies the stability of an n-dimensional system. Run: python3 platooning.py

The cars are controlled to maintain equal distances. Real case example: https://youtu.be/7wm-pZp_mi0

Three parameters can be tuned:

  • the number of cars « m »,
  • the disturbance amplitude « w_i »,
  • the scale factor of the ellipsoid Q « q_i ».

The code will also simulate the platooning and display two Figures: an animation of the cars and a plot of the states over time.

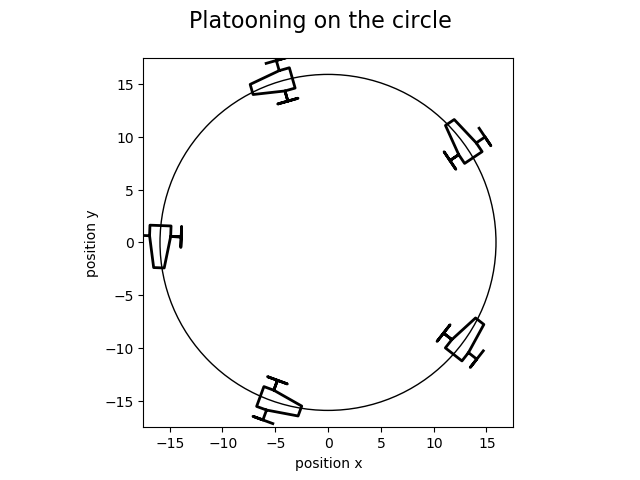
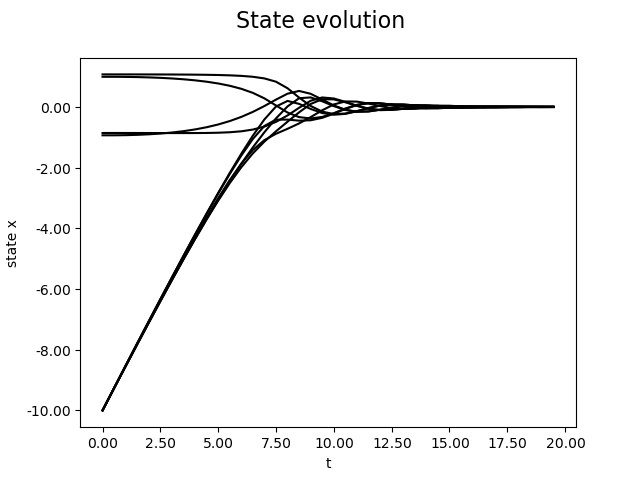
Blank Model

Follow the instructions in blank_model.py to use the enclosing method on your system.

Toolbox

Tools developed for the enclosing method are in lib/enclosing_method_toolbox.py. The main class is PositiveInvEllipseEnclosureMethod.